AUDIO OUTPUT TRANSFORMERS

An audio transformer can be modeled as below. Image courtesy of Igor Popovich

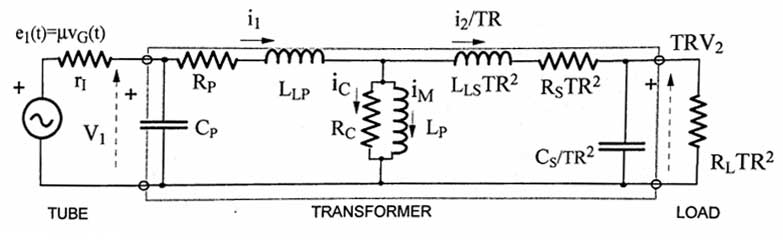
r_i = anode resistance of output tube
C_p = capacitance of the primary winding
R_p = resistance of primary windings
L_LP = leakage inductance of the primary winding
R_c = core power losses, due to eddy currents and hysteresis
L_p = primary inductance
L_LSTR² = leakage inductance of secondary reflected to the primary side. TR = turns ratio
R_sTR² = secondary resistance reflected to the primary side
C_s/TR² = parasitic capaticance of secondary reflected to the primary side

The parallel combination of Rc and Lp is the transformer itself. Now, this is a very complicated model to analyze, so it will be analyzed for the Low frequency model, midfrequency model, and HF model.

MID-FREQUENCY MODEL

At mid-frequencies (100 - 5000Hz), all inductances and capacitances can be pretty much ignored, so you're left with just a simple voltage divider:
V_o = R_LTR² / (r_i + R_p + R_sTR² + R_LTR²).

LOW FREQUENCY MODEL

At low frequencies (200Hz to 5kHz) the inductances and capacitances can be ignored except for L_p. So you're left with the following simplified model:

where R1 = r_I + R_p and R2 = (R_s + R_L)TR²

Now the frequency where the output voltage drops by 1/√2 relative to the midband gain is the -3dB frequency f_L. This frequency is determined by the following:
f_L = [R₁R₂TR² / (R₁ + R₂TR²)]/2πL_p, or more simply
f_L = (R₁ ∥ R₂TR²) / 2πL_p       ∥ means "parallel with"
Or, even more simply:
f_L = R_PAR / 2πL_p,    where R_PAR = R₁∥R₂TR²    

Remembering that R₂TR² = primary impedance of XFMR, also known as Z_P:
R_PAR = R₁ ∥ Z_P.     Now, r_I >> R_p, so R_p can be ignored (it's usually less than 100). Thus:
R_PAR = r_I ∥ Z_P

So, finally;

You want f_L as low as possible, so you want L_P above a certain minimum. Rearranging the above, gives:
L_PMIN = R_PAR / 2πf_L

L_PMIN is the minimum value of L needed to get the lower -3dB frequency f_L to the desired level to allow for adequate bass.
Looking at the above, a lower R_PAR means a lower (and easier to make) L_PMIN. This means that low impedance tubes (those with low r_I) are more desirable for the beginning output XFMR maker.

HIGH FREQUENCY MODEL

For reasons I don't fully get, the shunt capacitances of the transformer model can be ignored, so you are left with the following model.

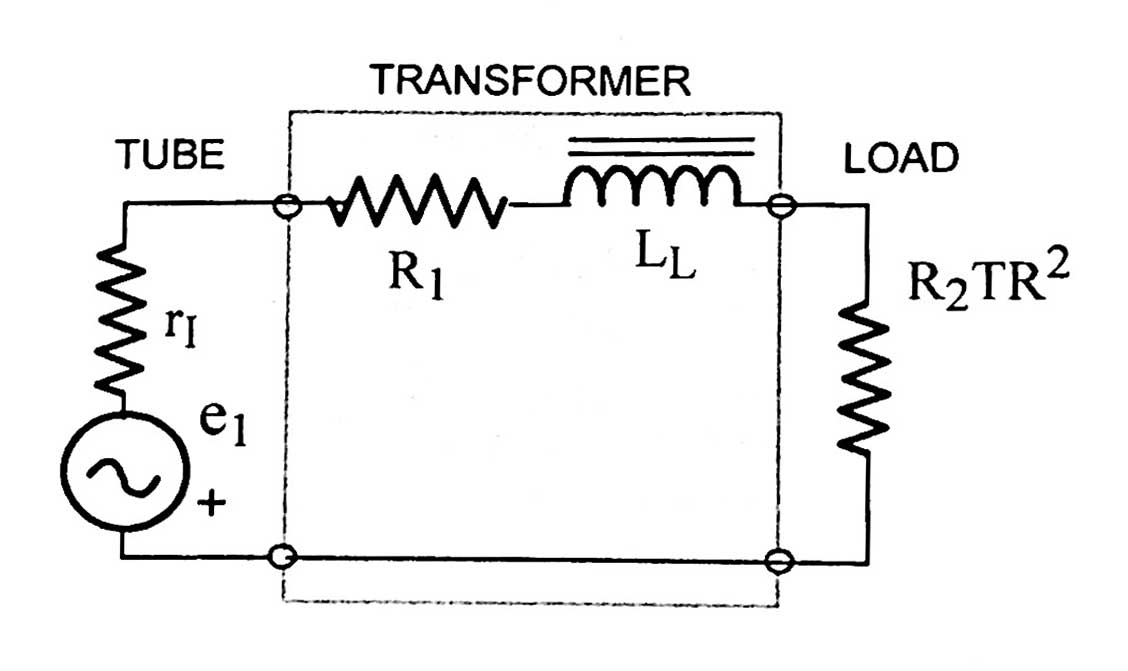
This is a simple low-pass LR filter and the upper -3dB frequency relative to the midband gain is the frequency at which the reactance of the total leakage inductance = resistance of the 3 resistors in series. In other words:
2πf_UL_L = R_SER,      where L_L = L_LP + L_LSTR² and    R_SER = r_I + R₁ + R₂TR². So...

f_U = R_SER/2πL_L
L_LMAX = R_SER/2πf_U

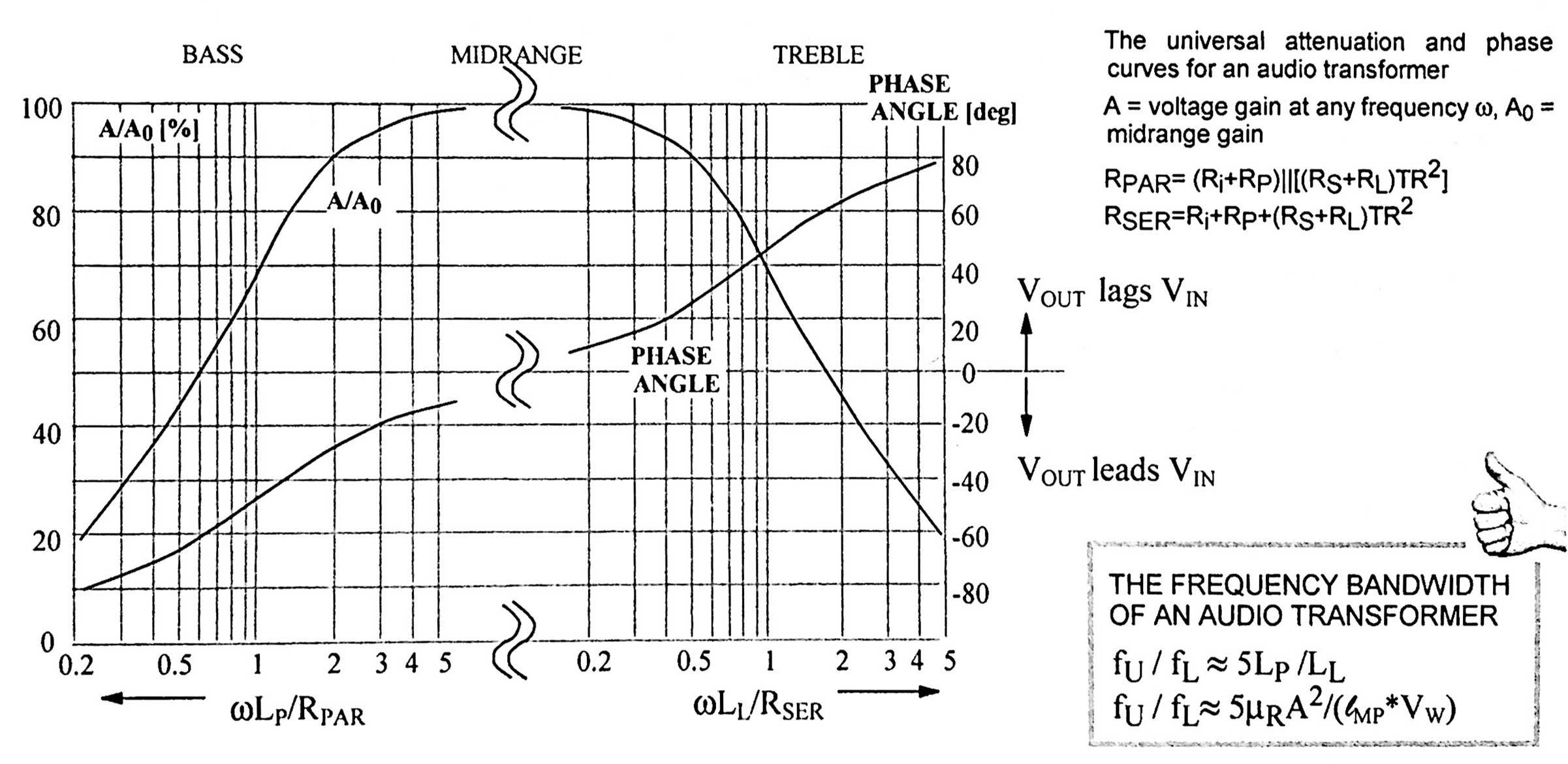
UNIVERSAL FREQUENCY AND PHASE RESPONSE CURVES

It turns out that if you look at values of R_PAR and R_SER, R_SER is usually about (and that's a very big about) 5X larger than R_PAR. So, looking at equations above, it's easy to see that:
f_U / f_L = 5L_p / L_L

All the above can be summed up in a graph below, found in Igor Popovich's book "Transformers for Tube amplifiers." Note that for both the high-frequency and the low-frequency halves, the gain has dropped to .707 (1/√2) when ωL = R

LEAKAGE INDUCTANCE

Leakage inductance L_L is due to magnetic flux between primary and secondary windings that is not coupled through the magnetic core. If L_L = 0, then all of the flux is shared by the windings. A sad fact of life is that as f increases L_L increases.

Without going through a derivation (which I don't know anyway), the following expression is given:
L_L = u₀VN_p²/CL²,    where V = volume between the windings, CL = coil length, N_p = number of turns.

Note that L_L is not dependent on the permeability of the iron or the induction levels. L_L decreases as the lamination size increases (increasing CL).  L_L increases with the volume V between the windings, which is partly determined by the insulation thickness. A way to reduce V is to use bulk winding, as opposed to layered arrangements, which decreases the insulation between layers. L_L increases quickly as the number of turns increases.

So the opposing goals: increasing NP increases Lp and affords better bass (f_L decreases), but it also increases L_L which hurts treble (f_U decreases).

This can be summed up by the equation at the bottom right of the frequency curve above. This equation is derived as follows:
L_P = N_P²μ_Rμ₀A/ℓ_MP    (see the Transformer Theory page)
L_L = μ₀N_P²V_W/A,     where V_W = volume of the windings (see above).
So, f_U / f_L = 5L_P / L_L = 5μ_RA² / (ℓ_MPV_W)

This equation shows that increasing cross-sectional area A of the laminations seems to increase the bandwidth, but this is offset by the increase in ℓ_MP and V_W, so the only real way of increasing bandwidth is to increase permeability by using high quality iron.

Looking at the equations for f_U and f_L, the following is seen:
On the low frequency side, you want to minimize r_I and maximize L_P.
Unfortunately on the high frequency side you want to maximize r_I. This favors pentodes and tetrodes. L_P doesn't really matter, but you want to minimize L_L.