CHOKE DESIGN STEPS

1. First determine A based on desired inductance and maximum current allowed:
A = 27.5*I*√L

2. Next, calculate NI based on A, using the graph below.

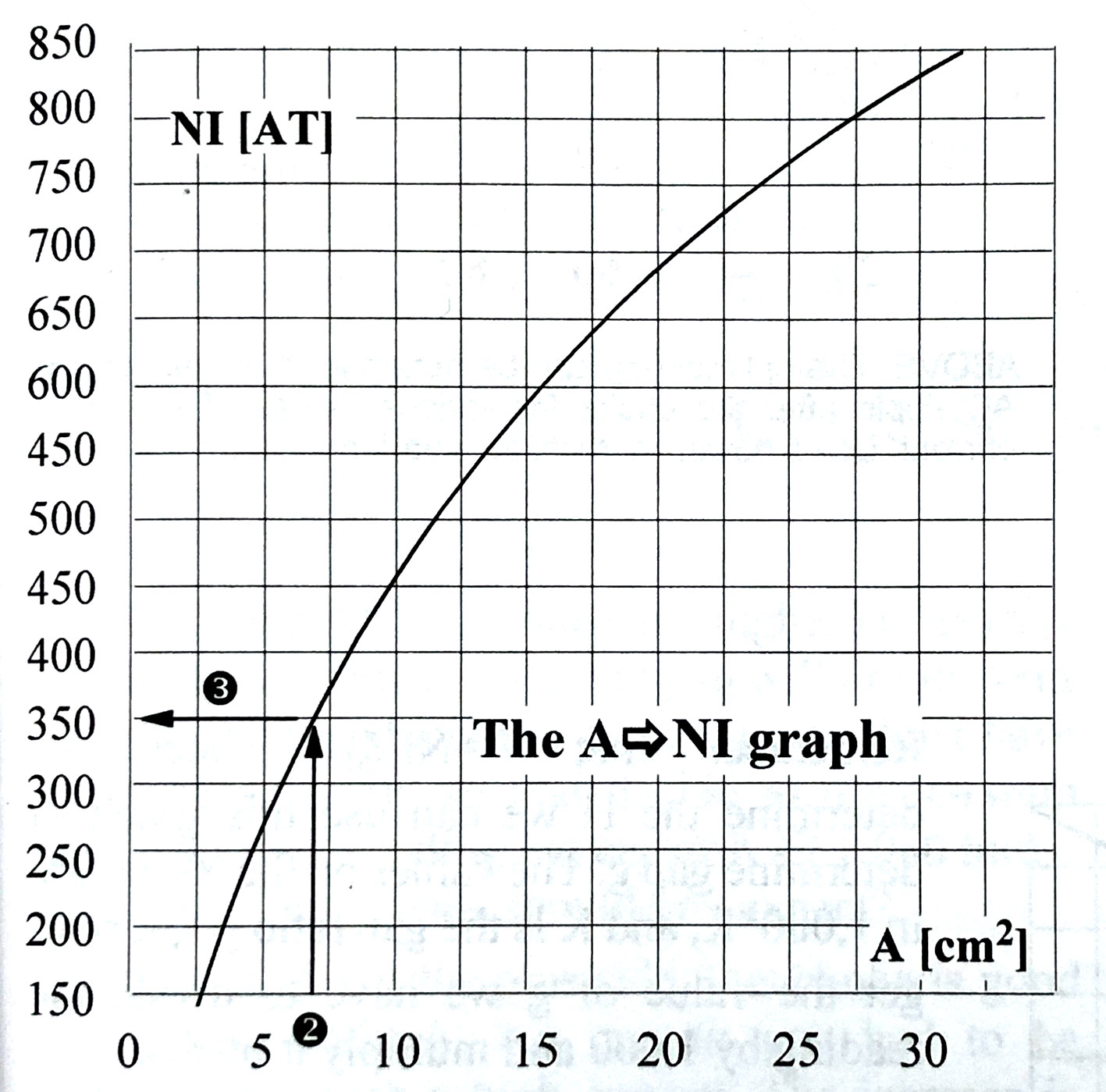
3. Calculate number of turns based on maximum I allowed. For example, in above NI = 350. If I_max = .12ma, then N=2917.

4. Next, figure out if this number of turns will fit onto the bobbin.

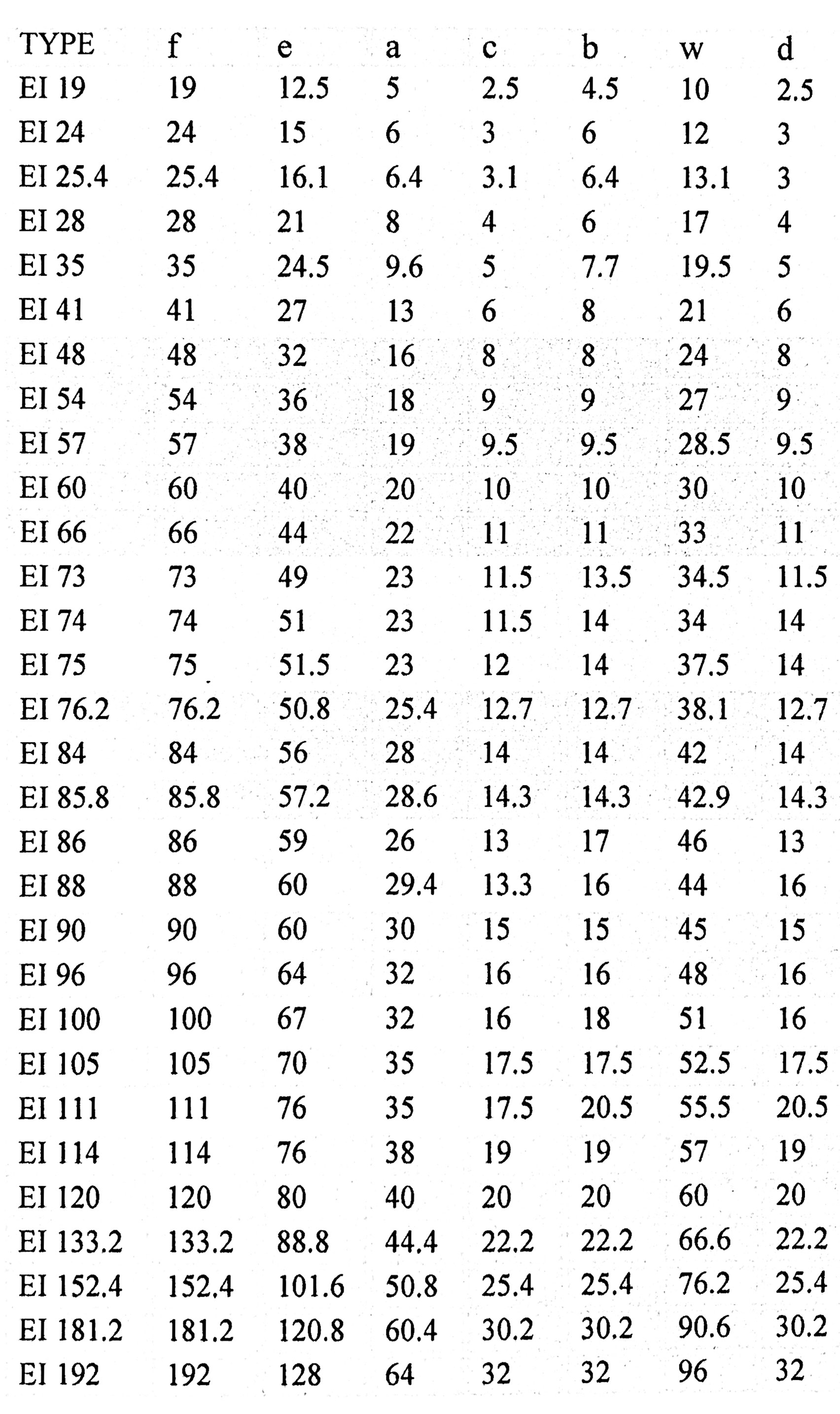
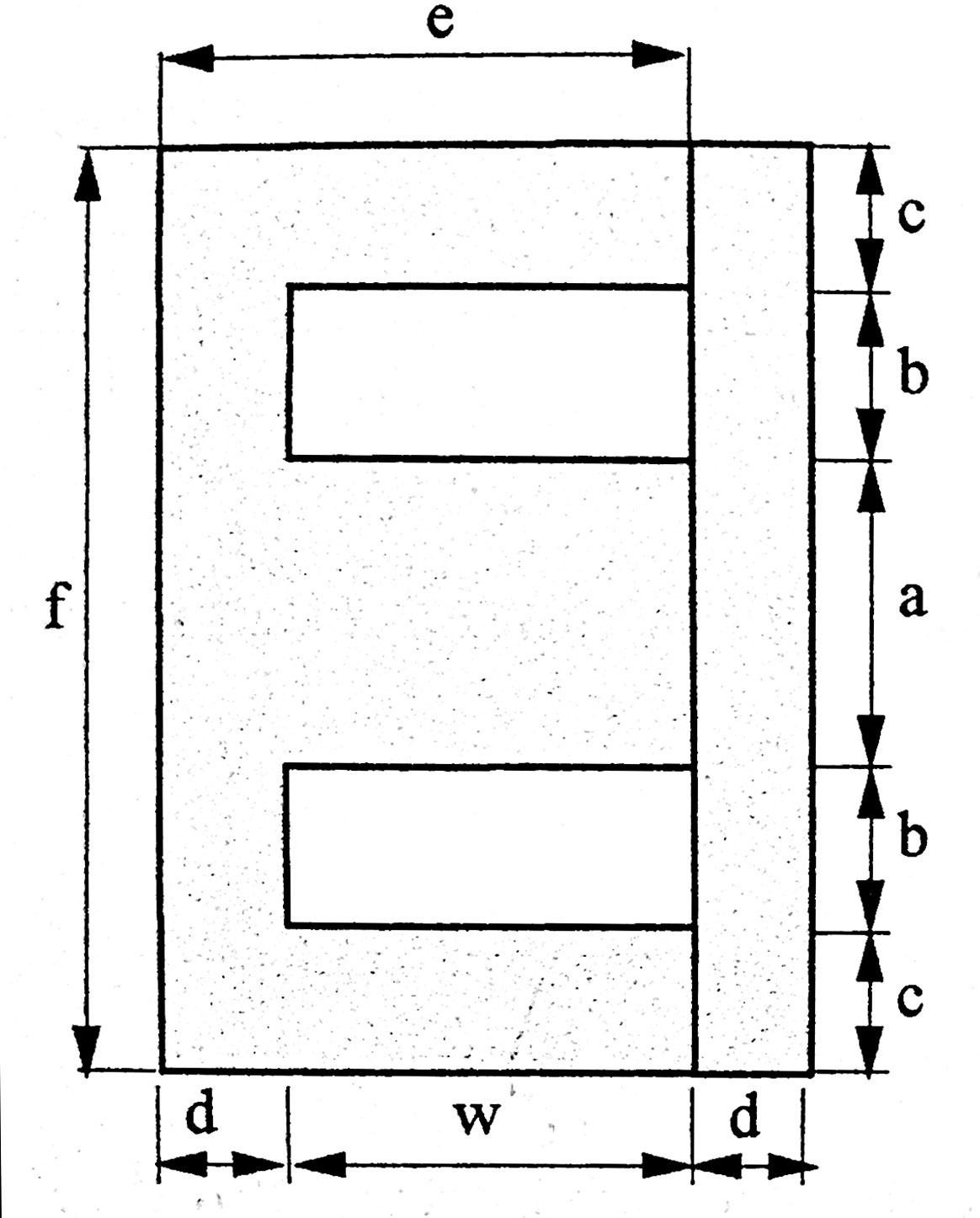
Above are 2 views of an E-I core (no gap shown). The area marked WH x WL is the area where the wires have to fit. Note that this is also b x w. The bobbin has thickness BT(usually about 2mm). On top of the wires is a top insulation layer and a top clearance (usually about .5mm for both)

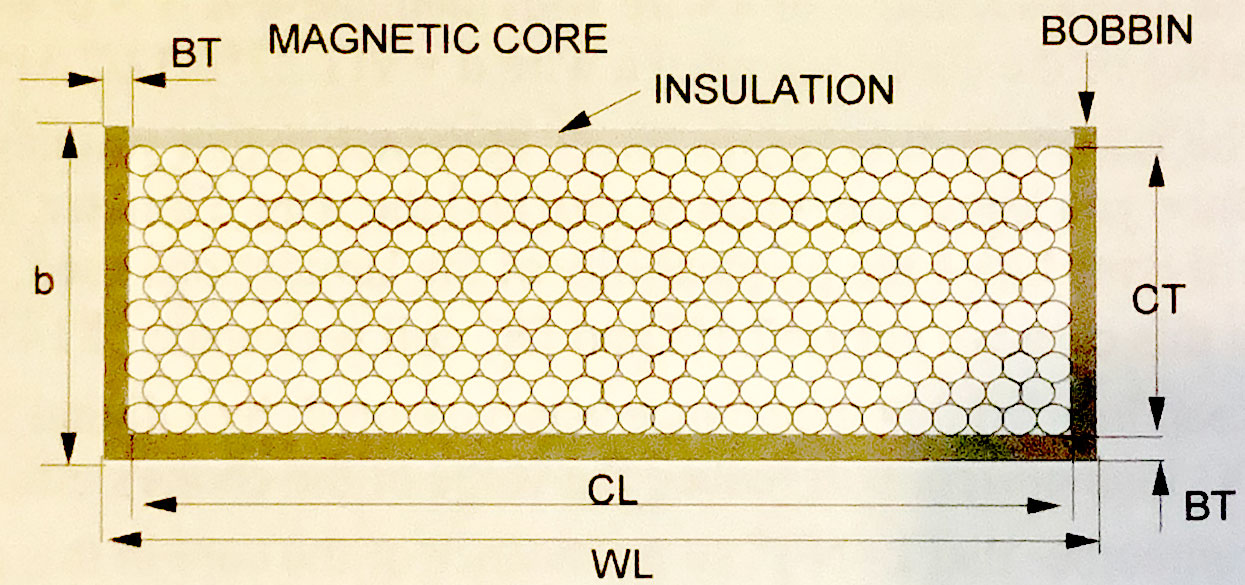
So the coil thickness CT = b - BT - .5mm.
and the coil length CL = w - 2BT
The net winding area NWA = CT * CL
Now
d = diameter of wire in mm, and this should be published.
d+.02 = width of wire with insulation
So GA = (d+.02)² = area of wire if you assume wire is square, which it isn't, BTW.
If the wire diameter WITH insulation is published, then you don't need to add the .02mm.
Assuming square wire, you can fit the following number of turns in the net winding area NWA:
N_N = NWA / GA
N_R is the realistic number of turns that can be fit into the NWA and is determined by skill of winder.
N_R = .9 * N_N for a skilled winder, .8 or .7 is used for less skilled winder.

EXAMPLE:
You are using EI60 laminations, so from above table
w=30mm and b=10mm. Assuming bobbin thickness of 2mm ->
CL=30 - 4 = 26mm and CT = 10 - 2 - .5 = 7.5mm, so
NWA = 26 * 7.5 = 195mm²
You have wire with diameter .25mm, and you assume an insulation thickness of .02mm, so
GA = .27² = .073mm²
N_N = 195/.073 = 2671 turns.
Assuming a semi-skilled winder
N_R = .9*2671 = 2404 turns.

Next, figure out the total length of wire. This will allow a calculation of the resistance R of the inductor. The MLT is the mean length of a turn, so multiplying this by the number of turns should give the total length of the wire
L_W = MLT * N_R
The formula for MLT, for chokes is
MLT = 2/(a+S+4*BT) + π*CT, where S=stack thickness and other variables were described above.
So in the above example, if the stack thickness is say, 25mm,

MLT = 2/(20 + 25 + 4*2) + π*7.5 = 129mm

We can now figure out the resistance of the length of wire:
First, calculate the total length of the wire
L_W = MLT x N_R = 2404 x 129mm = 310116mm = 310.116m

R_C = ρ * L_W / πr²,      where, from above, r = d/2 = .125mm = .000125m and ρ = resistivity = 1.68 X 10^-8 Ω-m for copper.

R_C = 1.68 x 10^-8Ω-m   x  310.116m   /  π(.000125m)² = 106.1 Ω

This is a nearly finished E-I transformer. A bobbin with wire wound around it is fit onto the center leg of the E-piece, then the stack of I pieces (darker brown in photo to the left) is put in place.

The Magnetizing Force or Magnetic Field Strength H is defined as:
(1)   H(t) = i(t) * N / ℓ_MP     where N=number of turns, ℓ_MP = mean magnetic length, described below

The flux density B is the Magnetizing force H multiplied by the permeability μ of the core, where μ = μ_R*μ_O
μ_R = relative permeability = 1 for air, much higher than 1 for ferromagnetic materials.
μ₀ = absolute permeability = 4π*10^-7, so
(2)   B(t) = μ_R*μ_OH(t)  

Magnetic flux Φ is the flux density B x the cross sectional area A of the core.
(3)   Φ(t) = B(t) *A
(4)   Φ(t) = μ_R*μ_OH(t) * A
(5)   Φ(t) = μ_R*μ_O*i(t)*N*A/ℓ_MP

Now the induced voltage is proportional to the derivative of the flux Φ(t) and is negated.
        V(t) = -N * dΦ(t)/dt
Using equation (5):
         V(t) = -N²Aμ_R*μ_O/ℓ_MP * di/dt
Now, this is the familiar inductance equation with:
(6)   L = N²Aμ_R*μ_O/ℓ_MP

For any sinusoidal wave,
(7)   Φ(t) = Φ_maxsinwt

As in equation (7), V(t) can be expressed as V(t) = V_max*sin(wt), or alternatively
(9)   V(t) = -V_max*cos(wt)

Comparing (8) and (9), we see that
(10)   V_max = wNΦ_max

From equation (3)
(11)   Φ_max = A * B_max

so, combining (10) and (11)
(12)   V_max = wNAB_max = 2πfNAB_max

Rearranging (13), can give the turns per volt (TPV)
(14)   TPV = N/V_rms = 10⁴ / (4.44fNAB_max)

SPECIAL CASE FOR E-I LAMINATIONS:

For E-I laminations:
(15)   TPV = k/A_EF, where k is a published number:
50Hz: k=45, GOSS k=40
60Hz: k=37.5, GOSS k=33.3
Rearranging:
k = TPV * A_EF
Substituting equation (14) and using A_EF for A :
(16)   k = 10⁴ / (4.44fNB_max)

ELECTRICAL ANALOGY

Recalling equation (1), for DC it is
(17)   H = NI/ℓ_MP

Now, NI is called the magnetomotive force (MMF) or ampere-turns (AT). It is also called the total field. It is analogous to voltage in an electrical circuit. It is what pushes the flux Φ through the core. This can be expressed as:
(18)   MMF = Φ * R,     where R is called the reluctance.

Figure out what R is:
Rewriting equation (18) => R = MMF / Φ = NI / Φ
Substituting equation (5) gives:
          R = NI / (μINA/ℓ_MP)    where μ = μ_R*μ_O
(19)   R = ℓ_MP/μA

So high-permeability materials have low R, so the core presents a low magnetic resistance to magnetic flux, thus very little flux excapes the core into the surrounding air, which has a very high reluctance.

The inverse of reluctance R is called the permeance P and is the inverse of R:
(20)   P = μA / ℓ_MP

Looking at equation (6), it is easy to deduce that:
(21)   L = N²P

THE GAP

Without looking at all the hysteresis curves and permeability curves, suffice it to say that DC current through the core as in a choke or SET output transformer leads quickly to saturation of the core. So an air gap is placed to increase the reluctance. Air has a permeability of 1. The grueling calculations are below.

From (18), and remembering that MMF = NI
NI = Φ(R_g + R_c)
      = Φ[g/(μ_OA_g) + ℓ_MP/(μ_Rμ_OA_c) ]
      = Φ/A *[g/μ_O + ℓ_MP/(μ_Rμ_O)      this assumes A_c=A_g, which is not exactly correct because of fringing.
      = B*[g/μ_O + ℓ_MP/(μ_Rμ_O)      from equation (3)

Divide both sides by ℓ_MP and remember that H = NI/ℓ_MP you get:
H= B * [g/(μ_Oℓ_MP) + 1/(μ_Rμ_O)]

From equation (2) H = B * 1/μ, so......
H = B * 1/μ_EF, where
1/μ_EF = 1/[g/(μ_Oℓ_MP)+ 1/(μ_Rμ_O)]

Things get a little easier for chokes (or transformers) with a gap. A typical μ_Rμ_O for the core may be in the neighborhood of 10,000 while the μ for the gap is 1. For, say, EI66 laminations, a typical gap is .15mm and a typical ℓ_MP is maybe 12cm and A=6.8.
So, from equations (22) and (23),
R_c = 12/(10000*6.8) = 1.77x10^-4
R_g = .15/6.8 = 2.2x10^-3
So the reluctance R_g of the gap is 12 times the reluctance of the core, so is the overwhelming determinant of total reluctance.

EXAMPLE